Emotion Recognition In the Wild (EmotiW) is a competition organized under the umbrella of International Conference on Multimodal Interaction (ICMI). The competition is being organized since 2013. The competition for the year 2017 consisted of two sub-challenges :
- Group Level Emotion Recognition
- Audio-Video Emotion Recognition
I participated in the former with Bhanu Pratap Singh Rawat and Manya Wadhwa. We were given a dataset which contained photographs of groups of people. The aim of the sub-challenge was to come up with a model that could classify the emotion the group as Positive, Negative or Neural. This post describes our approach for the challenge.
Dataset
The dataset was divided into three parts: train, validation and test. Each part consisted of image files for each of our target categories: Positive, Negative or Neutral. The distribution of images in the dataset is:
| Set | Positive | Neutral | Negative | Total |
|---|---|---|---|---|
| Train | 1272 | 1199 | 1159 | 3630 |
| Validation | 773 | 728 | 564 | 2065 |
| Test | 311 | 165 | 296 | 772 |
A sample of images from the dataset is given below:

Method
Summary: We used ConvNets for our task with emotion heatmaps as features. If you wish to know the specifics of what emotion heatmaps are, read on!
Emotion of Individual Faces
The first step of our approach was to extract faces from each file and determine the emotion of each face. We extracted faces from the files using Dlib and determined the emotion for each of the extracted faces. This was done using the pre-trained models by Gil Levi and Tal Hassner developed for EmotiW 2015 (we shall refer to them as LHModels throughout the post). It is a set of five models which assign scores for seven standard emotions: Anger, Disgust, Fear, Happy, Neutral, Sad and Surprise. A single score for each face across the seven categories is obtained by averaging the five scores obtained for each category.
Combination of Values
Once we obtained face wise emotions, a logical next step was to use the scores obtained for individual faces and somehow combine them to enable a learning algorithm to accurately determine the emotion of a group.
We averaged five vectors obtained for every face in the image. The emotion with the highest value was said to be the overall emotion of the group. We then trained a Random Forest Classifier (15 estimators) with the averaged seven-dimensional vector for each image.
For both of the cases above, if an image was labeled as one of Anger, Disgust, Fear, Sadness or Surprised the final label assigned to it was Negative, Neutral was assigned Neutral and Happy was assigned Positive. The performance for each of the approaches is summarized in a table later.
We then used the predictions of LHModels to generate heatmaps for our images. The first step was to convert the seven-dimensional vectors into three-dimensional vectors representing our three categories of interest, Positive, Negative and Neutral. We did this by taking the average of Anger, Disgust, Fear, Sadness and Surprised designating it the label Negative, Happy was given the label Positive, and Neutral was assigned Neutral.
After this step, we had a set of three values for every face (one corresponding to each emotion). We used those to create three heatmaps, which, actually, are Gaussian interpolations of those values in a two-dimensional space. The code snippet below creates a two-dimensional Gaussian kernel. The height and width of the kernel are same as that of the image in which the face was present. When interpolating, we observed that the values fell quickly as we went away from the center of the heatmap, since the distance increases rapidly. We used a value of 0.1 to make the values decrease gradually over distance (in other words, the effective distance from one pixel to the next was reduced to 1/10th of its original value).
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import numpy as np
DISTANCE_SMOOTHING = 0.1
def make_gaussian(width, height, center=None, fwhm = 3):
""" Make a square gaussian kernel.
fwhm is full-width-half-maximum, which
can be thought of as an effective radius.
"""
x = np.arange(0, width, 1, float)
y = np.arange(0, height, 1, float)
y.shape = (height, 1)
if center is None:
x0 = y0 = size // 2
else:
x0, y0 = center
return np.exp(-4 * np.log(2) * ((DISTANCE_SMOOTHING * (x-x0)) ** 2 + (DISTANCE_SMOOTHING * (y-y0)) ** 2) / fwhm ** 2)
The kernel is then multiplied by the value of the emotion for that face. Let us take the face below as an example:

The heatmaps (2D Gaussian distributions) for Negative, Positive and Neutral emotion values for the above face are:
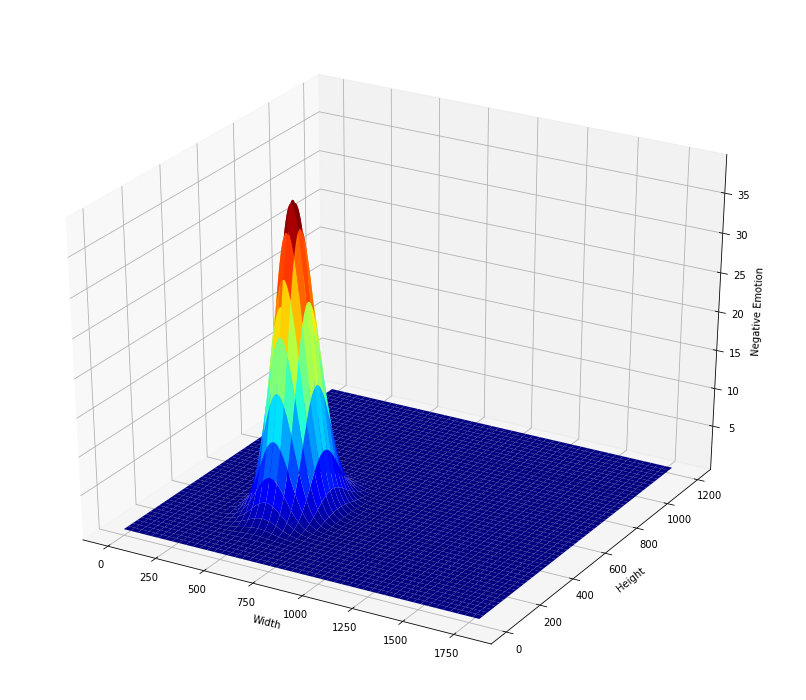
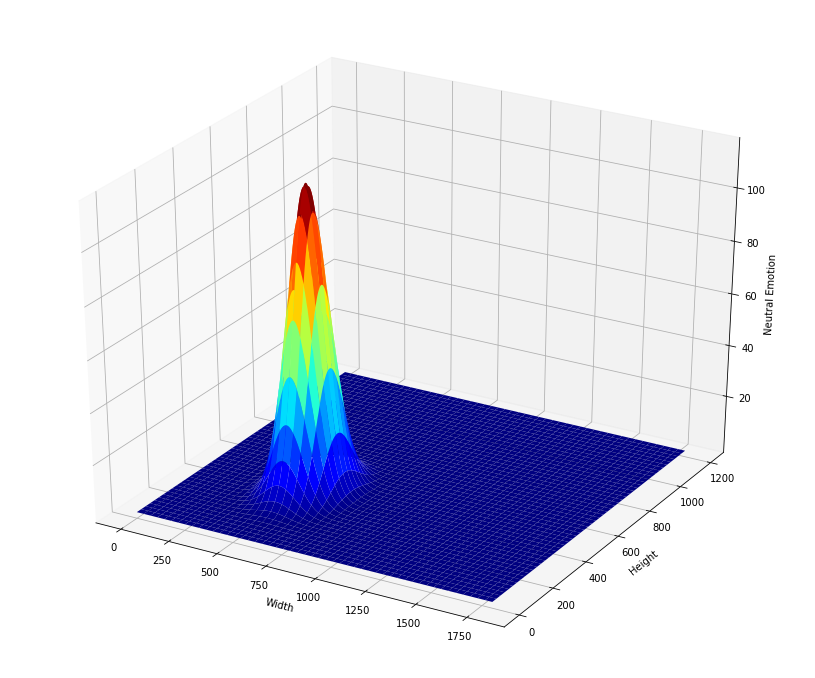
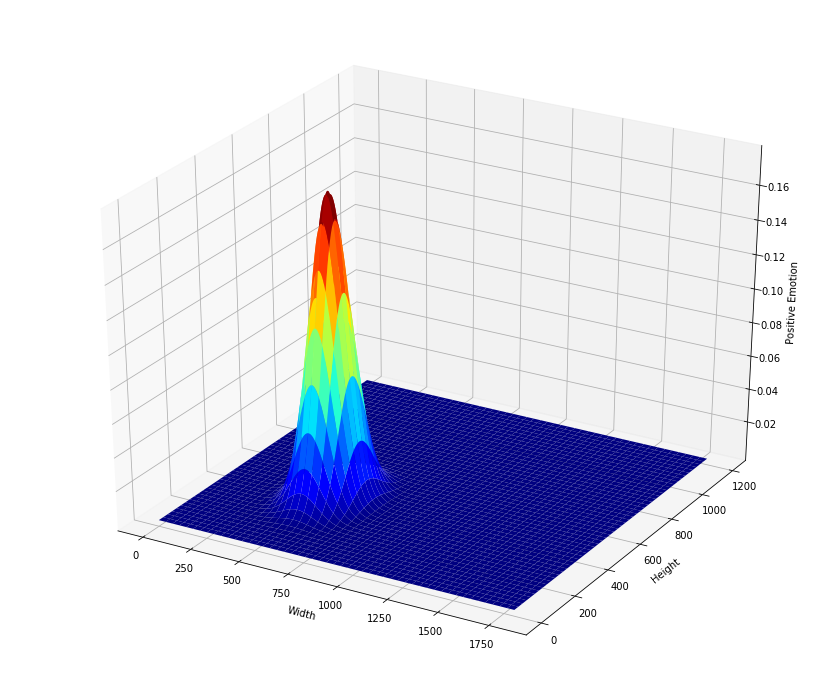
We, then used the individual heatmaps as channels of an RGB image, with distribution for Negative emotion being the red channel and those of Neutral and Positive forming the green and the blue channels respectively. For the face shown above, the final heatmap looks like the image below:

We carry out this process for every face in an image and finally add the RGB images tensor together, thus forming a single image.
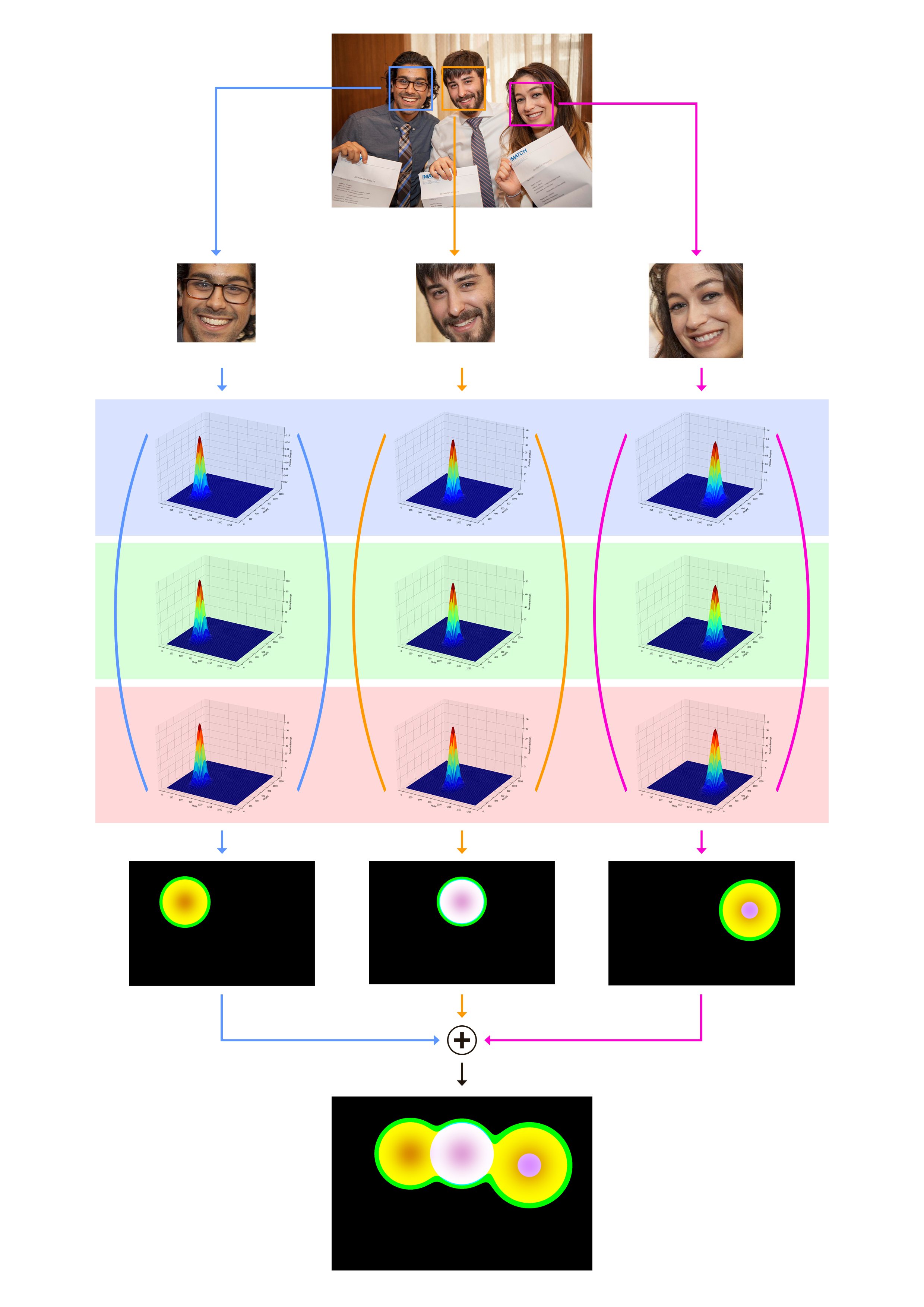
The image above demonstrates the entire process of converting an image to a heatmap. The final heatmap was then resized and fed to Convolutional Neural Networks. Using this methodology, we achieved a classification accuracy of 56.47% on the validation set. The baseline was 52.79%.
A table summarizing the performance of the approaches is given below.
| Model | Training Accuracy | Validation Accuracy |
|---|---|---|
| Baseline | - | 52.79% |
| Averaging | 44.37% | 42.38% |
| Random Forest | 99.08% | 48.13% |
| ConvNet on Heatmaps | 54.16% | 56.47% |
Please refer to our paper for more details.
Comments